4種水稻葉面積測量方法的差異對比
三種測水稻葉面積的方法介紹:
(1)繪圖剪紙稱重法:
(2)長寬相乘分級折換法,長寬比為2012.5的及其以下的用7折換,2512.5的用0.79折換,3012.5的及其以上的用0.78折換,
(3)梯形積加法,將葉片壓平展,由葉尖到基部,每隔5厘米測量其寬度,分段計算面積(頂尖一段按等腰三角形計算,其余各段均按等腰梯形計算),然后積加成葉面積。
采用上述方法,經(jīng)整理分析后,可看出以下結(jié)果:
(一)按繪圖剪紙稱重法計算40張葉片的面積,得出葉片長方形面積折合成葉面積的折換值為0.637-0.8057,平均值為0.739,絕大多數(shù)在0.68-0.79的范圍內(nèi),表明不同的葉形折換值應(yīng)有所不同,一般用7-0.8折換,基本上可概括大部分的葉型。
(二)折換值與葉長度無明顯的關(guān)系,但仍表現(xiàn)出折換值大的長葉片多些,折換值與葉寬度沒有什么關(guān)系。
(三)折換值與葉最寬處離基部距離的相對值(變異范圍為15.6-67.5,平均值34.1)有一定關(guān)系,即折換值小的離基距相對值多數(shù)偏大些,但其相關(guān)系數(shù)僅為0.182,經(jīng)測繪未達到顯著標準。因此,不能認為離基距相對值可以作為決定折換值的標準。
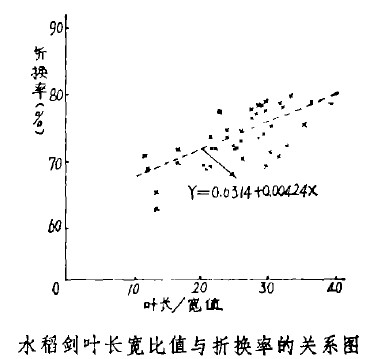
(四)折換值與葉片長寬比值有明顯的相關(guān)性,除少數(shù)葉片外,一般是長寬比值大的折換值也較大,長寬比值小的折換值也小。經(jīng)過計算,其相關(guān)系數(shù)為0.7511.經(jīng)“t”驗證,達到了極顯著的水平,即折換值的大小可以根據(jù)葉的長寬比值而定。為此,進一步求得回歸方程為:
Y=0.6314}0.00424X,經(jīng)用回歸系數(shù)的“t”
測定,證明是極顯著的,即折換值與葉長寬比的回歸關(guān)系可以成立(見圖)。
為了驗證用上述回歸方程計算出的折換值,用以計算葉面積是否符合各種葉形的實際,又對用上述三種方法計算出的40張葉片的葉面積和用回歸折換值計算的葉面積進行比較,可以看出:
(1)四種方法所得出的葉面積值,總的說,都基本接近,所得的葉面積相互間差異都很小(1厘米z以下),差異達1-3厘米2的占絕對少數(shù),四種方法所得葉面積分葉片測定其適合度,Xz值均很小(未達到1以上),說明四種方法所測得的葉面積值比較一致,無顯著差異,四種方法測得葉面積平均數(shù)的標準差,只有5片葉超過1,其中有2片葉面積平均數(shù)的標準差超過了該平均數(shù)的5%以上,40張葉片四種方法的平均值差異更小。總之,除少數(shù)葉片外,一般四種方法之間差異較小。
(2)如以繪圖剪紙稱重法所測葉面積作標準(對照),分別與其它三種方法相比較,則長x寬x分級折換值所測得的葉面積差異較大,40張葉片中有11片(占27.5%)的葉面積與對照差異達到5%以上,用回歸折換值所得葉面積,有4片葉(占10%)與對照的差異達到5%以上,梯形積加法所得葉面積有2片葉(占5%)與對照的差異達到5%以上。可見,梯形積加法僅次于繪圖剪紙稱重法,比較可靠;其次是用回歸折換值計算葉面積的方法,用分級折換值計算葉面積的可靠性較差。因此,大量測量葉面積時,以先測量葉片的長寬度,再用上述回歸折換值計算葉面積,比較可靠而快速,簡便易行。
折換值為什么可用葉片的長寬比來決定?在實際測量葉面積的過程中可以看到,一般葉片長而窄(即長寬比大),其全部葉片中有比較長一段葉片的寬度接近于長條形(即長x寬),相反,葉片短而寬(即長寬比小)的,其最寬點或接近最寬度的只占很短一段,飛并常接近于葉基部,面積較接近于細長的等腰三角形。·所l-a,‘利用叮長寬相乘折換成葉可而,前者的折換值要大些,后者要小些。因此,用、葉長x葉寬x折換值的方法計算水稻葉面積時廠此折換值應(yīng)根據(jù)長寬比值而定,這樣的折換值才比較符合每一葉片的實際。·目前缺少測量儀器,四級農(nóng)科網(wǎng)可以廣泛采用此種方法,開展研究工作。




